There are times when you need to do something simple from the logic point of view but a bit exhausting when it comes to the sum of calculations you need to perform. I'm referring here to the past times (like 3-4 years ago) when I was forced to do all my circuit calculations manually without using anything except paper, pen and a calculator (without the solve function :-)). Hopefully now when I need to do some circuit calculations (which happens very rarely - thank God!) I'm allowed to use some computer software like MATLAB, Mathcad etc. However every single piece of software has it own environment and something like own programming language. So the question is how to use it properly, to speed your work and limit it to writing the logic and forcing computer to do the calculations.

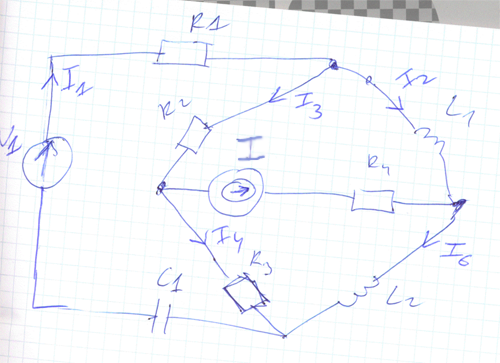
Figure 1. Sample circuit

Figure 1 shows a sample circuit which is going to be analyzed. So our task is to calculate all the unknown currents (I1,I2,I3,I4,I6) and voltage value of Uj. To compute the logic equations I'm using the Mesh analysis method (loop analysis) [1] which relies on Kirchhoff's circuit laws [2] (this little article is not a circuit theory tutorial so I hope the reader is familiar with those laws).

So the mesh equations (equations are the sum of the voltage drops in a complete loop of the mesh current) look like this (I=II - just another symbol for Matlab):

1) U1-I1*R1-I3*R2-I4*R3-I1*XC1=0
2) -I2*XL1+II*R4-Uj+I3*R2=0
3) Uj-II*R4-I6*XL2+I4*R3=0

And now the Kirchhoff's current laws:
 

4) I1-I3-I2=0
5) I3-I4-II=0
6) I4+I6-I1=0

So now there are at least two methods to put those equations into MATLAB or Mathcad and force them to calculate the values we need. In Mathcad we can use the Given-Find method [3,4] which basically solves the equations (as shown at the code listed below). When it comes to MATLAB we can use the symbolic 'solve' command [5] as shown at the corresponding MATLAB code below. Of course due to the fact MATLAB 'solve' command operates on symbols we need to convert the symbol values to numbers afterwards (this is done by the symbolic substitution command - 'subs'). I think the source codes are self-explanatory, so that's basically all. I have no idea if this is useful for other 'human' beings but well it's useful for me :-)
 

References:

[1] - http://www.allaboutcircuits.com/vol_1/chpt_10/3.html
[2] - http://en.wikipedia.org/wiki/Kirchhoff's_circuit_laws
[3] - http://www.imakenews.com/ptcexpress/e_article000733879.cfm?x=b9mFjBg,0,w
[4] - http://ecet.spsu.edu/Course-Materials/ECET1011/ECET1011_Lab01.pdf
[5] - http://people.clarkson.edu/~wilcox/ES100/eqsolve.htm